How (NOT TO) measure latency

Attila Mihaly BalazsApril 8th, 2014Last Updated: April 7th, 2014

1 85 4 minutes read

Latency is defined as

time interval between the stimulation and response

and is a value which is of importance in many computer systems (financial systems, games, websites, etc). Hence we – as computer engineers – want to specify some upper bounds / worst case scenarios for the systems we build. How can we do this? The days of counting cycles for assembly instructions are long gone (unless you work on embedded systems) – there are just too many additional factors to consider (the operating system – mainly the task scheduler, other running processes, the JIT, the GC, etc). The remaining alternative is doing empirical (hands on) testing.

Use percentiles

So we whip out JMeter, configure a load test, take the mean (average) value 土 3 x standard deviation and proudly declare that 99.73% of the users will experience latency which is in this interval. We are especially proud because (a) we considered a realistic set of calls (URLs if we are testing a website) and (b) we allowed for JIT warmup.

But we are still very wrong! (which can be sad if our company writes SLAs based on our numbers – we can bankrupt the company single-handedly!)

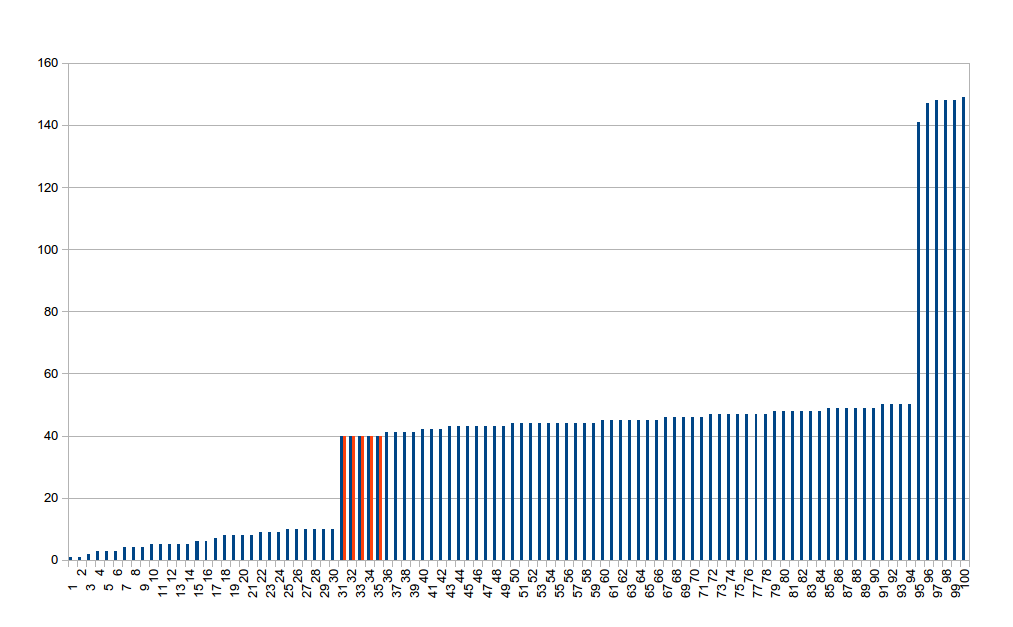
Lets see where the problem is and how we can fix it before we cause damage. Consider the dataset depicted below (you can get the actual values here to do your own calculations).

For simplicity there are exactly 100 values used in this example. Lets say that they represent the latency of fetching a particular URL. You can immediately tell that the values can be grouped in three distinct categories: very small (perhaps the data was already in the cache?), medium (this is what most users will see) and poor (probably there are some corner-cases). This is typical for medium-to-large complexity (ie. “real life”) composed of many moving parts and is called a multimodal distributions. More on this shortly.

If we quickly drop these values into LibreOffice Calc and do the number crunching, we’ll come to the conclusion that the average (mean) of the values is 40 and according to the six sigma rule 99.73% of the users should experience latencies less than 137. If you look at the chart carefully you’ll see that the average (marked with red) is slightly left of the middle. You can also do a simple calculation (because there are exactly 100 values represented) and see that the maximum value in the 99th percentile is 148 not 137. Now this might not seem like a big difference, but it can be the difference between profit and bankrupcy (if you’ve written a SLA based on this value for example).

Where did we go wrong? Let’s look again carefully at the three sigma rule (emphasis added):

nearly all values lie within three standard deviations of the mean in a normal distribution.

Our problem is that we don’t have a normal distribution. We probably have a multimodal distribution (as mentioned earlier), but to be safe we should use ways of interpreting the results which are independent of the nature of the distribution.

From this example we can derive a couple of recommendations:

Make sure that your test framework / load generator / benchmark isn’t the bottleneck – run it against a “null endpoint” (one which doesn’t do anything) and ensure that you can get an order of magnitude better numbers
Take into account things like JITing (warmup periods) and GC if you’re testing a JVM based system (or other systems which are based on the same principles – .NET, luajit, etc).
Use percentiles. Saying things like “the median (50th percentile) response time of our system is…”, “the 99.99th percentile latency is…”, “the maximum (100th percentile) latency is…” is ok
Don’t calculate the average (mean). Don’t use standard deviation. In fact if you see that value in a test report you can assume that the people who put together the report (a) don’t know what they’re talking about or (b) are intentionally trying to mislead you (I would bet on the first, but that’s just my optimism speaking).

Look out for coordinated omission

Coordinate omission (a phrase coined by Gil Tene of Azul fame) is a problem which can occur if the test loop looks something like:

start:
  t = time()
  do_request()
  record_time(time() - t)
  wait_until_next_second()
  jump start

That is, we’re trying to do one request every second (perhaps every 100ms would be more realistic, but the point stands). Many test systems (including JMeter and YCSB) have inner loops like this.

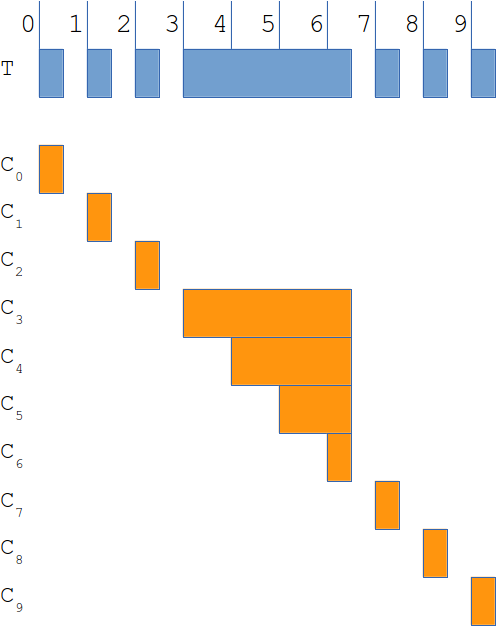
We run the test and (learning from the previous discussion) report: the 85% of the request will be served under 0.5 seconds if there are 1 requests per second. And we still can be wrong! Let us look at the diagram below to see why:

On the first line we have our test run (horizontal axis being time). Lets say that between second 3 and 6 the system (and hence all requests to it) are blocked (maybe we have a long GC pause). If you calculate the 85th percentile, you’ll 0.5 (hence the claim in the previous paragraph). However, you can see 10 independent clients below, each doing the request in a different second (so we have our criteria of one request per second fulfilled). But if we crunch the numbers, we’ll see that the actual 85th percentile in this case is 1.5 (three times worse than the original calculation).

Where did we go wrong? The problem is that the test loop and the system under test worked together (“coordinated” – hence the name) to hide (omit) the additional requests which happen during the time the server is blocked. This leads to underestimating the delays (as shown in the example).

Make sure every request less than the sampling interval or use a better benchmarking tool (I don’t know of any which correct for this) or post-process the data with Gil’s HdrHistogram library which contains built-in facilities to account for coordinated omission.