How to serialize an array of doubles with a byte (binary delta encoding for low-varianced monotonic sets of floating point data)
Low latency systems require high performance message processing and passing. As in most cases data has to be transfered over the wire or serialised for persistence, encoding and decoding messages become a crucial part of the processing pipeline. The best results in high performance data encoding usually involve applying knowledge of application data specifics. The technique presented in this article is a good example of how leveraging some aspects of the data benefits encoding in both latency and space complexity.
Usually the largest messages passed around high frequency trading systems represent some state of an exchange in a form of an excerpt from the order book. That is, a typical market data (tick) message contains information identifying an instrument and a set of values representing the top of the order book. A mandatory member of the data set is price/exchange rate information expressed in real numbers (for buy and sell sides).
What makes that data set very interesting from optimization perspective is that it is:
- monotonic
- low varianced
- non-negative*
So in practice we deal with sets of floating point numbers which are not only sorted (ascending for bid and descending for ask) but also having neighbouring values relatively “close” to each other. Keeping in mind that message processing latency is crucial for most trading systems, market ticks as one of key entities need to be passed as efficiently as possible.
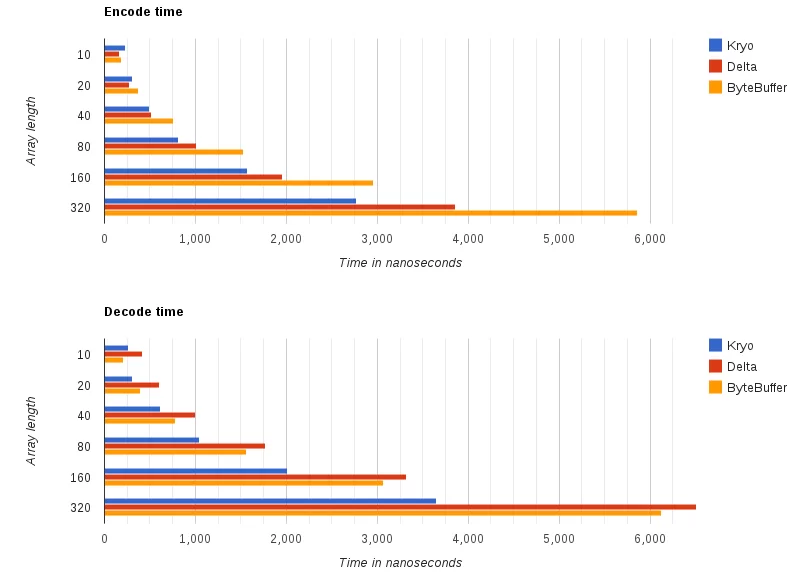
Let me demonstrate how all these features can be exploited to encode numeric data to a very compact binary form. First, two teaser plots demonstrating the difference between different serialization approaches:
So far we can see that delta encoding yields better results for encoding times as compared to standard ByteBuffer based serialization but becomes worse than Kryo (one of the most popular high-performance serialization libraries) as soon as we reach array lengths above 40. What is important here though, is a typical use-case scenario which for high frequency trading market messages happen to fit into the 10-40 range of array lengths
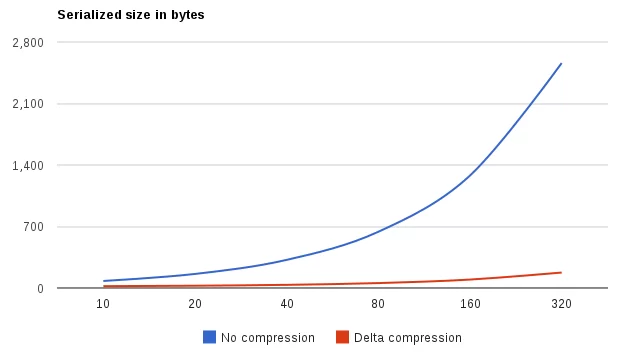
It gets much more interesting when we examine the resulting message sizes (as a function of array length):
The benefits of applying delta encoding should become obvious at this point (that blue curve applies equally to bytebuffer and Kryo serialization). What happens here is, with some knowledge on the specifics of data being processed it is safe to make assumptions that result in serialization being more CPU-intensive but ridiculously much more efficient space-wise. The idea behind delta compression is very simple. Let’s start with an arbitrary array of integral numbers:
- [85103, 85111, 85122, 85129, 85142, 85144, 85150, 85165, 85177]
If these were ints, without any compression we would have to use 4 * 9 = 36 bytes to store the data. What is particularly interesting in this set of numbers is that they are clustered relatively close to each other. We could easily reduce the number of bytes required to store the data by referencing the first value and then produce an array of corresponding deltas:
- Reference: 85103, [8, 19, 26, 39, 41, 47, 62, 74]
Wow! Now we can downsize to array of bytes. Let’s do the calculations again. We need 4 bytes for the reference value (which is still int) and 8 * 1 byte per delta = 12 bytes.
That’s quite an improvement from the original 36 bytes but there is still room for some optimisation. Instead of calculating deltas from the reference value let’s store differences for each predecessor successively:
- Reference: 85103, [8, 11, 7, 13, 2, 6, 15, 12]
The result is a non-monotonic set of numbers characterised by low variance and standard deviation. I hope it has already became clear where this is heading to. Still, it’s worth elaborating a little.
What we essentially ended up with at this point is a set that’s a perfect candidate for binary encoding. For our example that just means it is possible to accommodate 2 deltas in a single byte. We only need a nibble (4 bits) to accommodate values from 0-15 range so we can easily get away with ultimately squeezing the original array into 4 (for reference) + 8 * 1/2 = 8 bytes.
Since prices are expressed with decimal numbers, applying delta compression with binary encoding would involve establishing a maximum supported precision and treating decimals as integrals (multiplying them by 10 ^ precision), making 1.12345678 with precision of 6 a 1123456 integer. So far all of this has been a purely theoretical speculation with some teaser plots at the beginning of this article. I guess this is the right moment to demonstrate how these ideas may be implemented in Java with 2 very simple classes.
We’ll start with the encoding side:
package eu.codearte.encoder;
import java.nio.ByteBuffer;
import static eu.codearte.encoder.Constants.*;
public class BinaryDeltaEncoder {
public static final int MAX_LENGTH_MASK = ~(1 << (LENGTH_BITS - 1));
public ByteBuffer buffer;
public double[] doubles;
public int[] deltas;
public int deltaSize, multiplier, idx;
public void encode(final double[] values, final int[] temp, final int precision, final ByteBuffer buf) {
if (precision >= 1 << PRECISION_BITS) throw new IllegalArgumentException();
if ((values.length & MAX_LENGTH_MASK) != values.length) throw new IllegalArgumentException();
doubles = values; deltas = temp; buffer = buf;
multiplier = Utils.pow(10, precision);
calculateDeltaVector();
if (deltaSize > DELTA_SIZE_BITS) throw new IllegalArgumentException();
buffer.putLong((long) precision << (LENGTH_BITS + DELTA_SIZE_BITS) | (long) deltaSize << LENGTH_BITS | values.length);
buffer.putLong(roundAndPromote(values[0]));
idx = 1;
encodeDeltas();
}
private void calculateDeltaVector() {
long maxDelta = 0, currentValue = roundAndPromote(doubles[0]);
for (int i = 1; i < doubles.length; i++) {
deltas[i] = (int) (-currentValue + (currentValue = roundAndPromote(doubles[i])));
if (deltas[i] > maxDelta) maxDelta = deltas[i];
}
deltaSize = Long.SIZE - Long.numberOfLeadingZeros(maxDelta);
}
private void encodeDeltas() {
if (idx >= doubles.length) return;
final int remainingBits = (doubles.length - idx) * deltaSize;
if (remainingBits >= Long.SIZE || deltaSize > Integer.SIZE) buffer.putLong(encodeBits(Long.SIZE));
else if (remainingBits >= Integer.SIZE || deltaSize > Short.SIZE) buffer.putInt((int) encodeBits(Integer.SIZE));
else if (remainingBits >= Short.SIZE || deltaSize > Byte.SIZE) buffer.putShort((short) encodeBits(Short.SIZE));
else buffer.put((byte) encodeBits(Byte.SIZE));
encodeDeltas();
}
private long encodeBits(final int typeSize) {
long bits = 0L;
for (int pos = typeSize - deltaSize; pos >= 0 && idx < deltas.length; pos -= deltaSize)
bits |= (long) deltas[idx++] << pos;
return bits;
}
private long roundAndPromote(final double value) {
return (long) (value * multiplier + .5d);
}
}
A few words of introductory explanation before I go into details. This code is not a complete, fully-blown solution; it’s sole purpose is to demonstrate how easily it is to improve some bits of application’s serialization protocol. Since it is subjected to microbenchmarking it also does not induce gc-pressure just because the impact of even the quickest minor gc could severily skew the final results, hence the ugly api. The implementation is also highly sub-optimal, especially CPU-wise but demonstrating micro-optimizations is not the goal of this article. Having said that let’s see what it does (line numbers in curly brackets).
Encode method first does some fundamental sanity checks {17,18}, calculates the multiplier used in transforming decimals to integrals {20} and the delegates to calculateDeltaVector(). This in turn has two effects.
- Calculates rolling delta for the whole set by transforming decimals to integrals, subtracting from predecessors and finally storing the results in a temporary array {33}
- As a side effect works out the maximum number of bits required to represent a delta {34,36}
The encode() method then stores some metadata required for correct deserialization. It packs precision, delta size in bits and the array length in the first 64 bits {24}. It then stores the reference value {25} and initiates binary encoding {27}.
Encoding deltas does the following:
- Checks if it already processed all array entries and exit if so {40}
- Calculates the number of remaining bits to encode {41}
- Chooses the most appropriate type (given its size in bits), encodes the remaining bits, and writes the bits to the buffer {43-46}
- Recurses {47}
One last bit probably requiring some elaboration is the encodeBits() method itself. Based on type size (in bits) passed in the argument it loops over a temporary long which sole purpose is to serve as a bitset and writes the bits representing consecutive deltas moving from the most to the least significant part of the long value (scoped by the type size).
Decoding is, as expected, a pure opposite of encoding and is mostly about using the meta data to reconstruct the original array of doubles up to the specified precision:
package eu.codearte.encoder;
import java.nio.ByteBuffer;
import static eu.codearte.encoder.Constants.DELTA_SIZE_BITS;
import static eu.codearte.encoder.Constants.LENGTH_BITS;
public class BinaryDeltaDecoder {
private ByteBuffer buffer;
private double[] doubles;
private long current;
private double divisor;
private int deltaSize, length, mask;
public void decode(final ByteBuffer buffer, final double[] doubles) {
this.buffer = buffer; this.doubles = doubles;
final long bits = this.buffer.getLong();
divisor = Math.pow(10, bits >>> (LENGTH_BITS + DELTA_SIZE_BITS));
deltaSize = (int) (bits >>> LENGTH_BITS) & 0x3FFFFFF;
length = (int) (bits & 0xFFFFFFFF);
doubles[0] = (current = this.buffer.getLong()) / divisor;
mask = (1 << deltaSize) - 1;
decodeDeltas(1);
}
private void decodeDeltas(final int idx) {
if (idx == length) return;
final int remainingBits = (length - idx) * deltaSize;
if (remainingBits >= Long.SIZE) decodeBits(idx, buffer.getLong(), Long.SIZE);
else if (remainingBits >= Integer.SIZE) decodeBits(idx, buffer.getInt(), Integer.SIZE);
else if (remainingBits >= Short.SIZE) decodeBits(idx, buffer.getShort(), Short.SIZE);
else decodeBits(idx, buffer.get(), Byte.SIZE);
}
private void decodeBits(int idx, final long bits, final int typeSize) {
for (int offset = typeSize - deltaSize; offset >= 0 && idx < length; offset -= deltaSize)
doubles[idx++] = (current += ((bits >>> offset) & mask)) / divisor;
decodeDeltas(idx);
}
}The source code with some test classes can be found here. Please bear in mind even though it’s proven to work this code is certainly not production-ready. You can definitely make it work without requiring the temporary array, replacing full array scan when calculating max delta size with something clever or get away without that heavyweight division by doing division by reciprocal approximation. Feel free to pick those hints up or apply different micro-optimizations and build your own proprietary delta encoding protocol. It makes a vast difference for latency-sensitive trading applications reducing market data message size for liquid instruments by 20-30x. Of course you have to figure out yourself if switching to delta-compression binary encoding brings any value to your application ecosystem. Feel free to post comments with your findings!