Easy to understand Dynamic Programming – Edit distance
Following the topic of the last post, I will discuss another problem that can be solved efficiently using dynamic programming. Unlike the Fibonacci sequence that we saw on the introduction post, the problem that I present here is a bit more tricky to solve (which also makes it more interesting).
The reason I’ll review this problem and other similar ones in future posts is not just to show how to solve them. Anyone with access to google can search for one of the 100 already implemented solutions. The idea here is two show some key concepts that you can apply to any dynamic problem.
So lets start with the well known Edit distance problem. Basically, given two strings A and B, the edit distance measures the minimum number of operations required to transform one string into the other. In the most common version of this problem we can apply 3 different operations:
- Insert a new character into one of the strings
- Delete an existing character
- Replace one character by another
For example, given the strings A = “cat” and B = “cars”, editDistance(A,B) = 2 because the minimum number of transformations that we need to make is replace the “t” in A by “r” and then remove the “s” from B. After that, both strings are equal to “car”. Notice that in this case another possibility would have been to replace the “t” by an “r” but then insert an “s” into A, making both strings equal to “cars”. Similarly we could change both into “cat” or “cats” and the edit distance is still 2.
So how would we go about solving this problem? Lets try to solve a much smaller and simpler problem. Imagine we have the two previous strings again, this time represented as an array of chars in the general form:
A = [A0, A1, A2,…, An]
B = [B0, B1, B2,…, Bm]
Notice that the lengths of A and B (n and m respectively) might be different.
We know that in the end, both strings will need to have the same length and match their characters on each position. So, if we take just the first character of A and B, what choices do we have? We have 3 different transformations that we can apply so we have 3 choices as well:
- We can replace the first character of A by the first character of B. The cost of doing this replacement will be 1 if the characters are different and 0 if they are equal (because in that case we don’t need to do anything). At this point we know that both strings start with the same character so we can compute the edit distance of A[1..n] = [A1,…, An] and B[1..m] = [B1,…, Bm]. The final result will be the cost of transforming A[0] into B[0] plus the edit distance of the remaining substrings.
- The second choice we have is inserting a character into A to match the character in B[0], which has a cost of 1. After we have done this, we still need to consider the original A string because we have added a new character to it but we haven’t process any of its original characters. However, we don’t need to consider B[0] anymore because we know that it matches A[0] at this point. Therefore, the only thing we need to do now is to compute the edit distance of the original A and B[1..m] = [B1,…, Bm]. The final result will be this value plus 1 (the cost of inserting the character into A).
- The last case is symmetrical to the previous one. The third transformation we can apply is simply to delete A[0]. This operation has a cost of 1 as well. After doing this, we have consumed one character of A but we still have all the original characters of B to process. So we simply need to compute the edit distance of A[1..n] = [A1,…, An] and B. Again, the final value of the edit distance will be this value plus 1 (the cost of deleting A[0].
So which of the three choices should we pick initially? Well, we don’t really know which one will be better in the end so we have to try them all. The answer to our original problem will be the minimum value of those three alternatives.
The previous description is the key to solving this problem so read it again if it is not clear. Notice that, the last step on each of the three alternatives involves computing the edit distance of 2 substrings of A and B. This is exactly the same problem as the original one we are trying to solve, i.e., solving the edit distance for 2 strings. The difference is that after each decision we take, the problem becomes smaller because one or both input strings become smaller. We are solving the original problem by solving smaller sub-problems of exactly the same type. The fact that the sub-problems become smaller on each step is crucial to be sure that we’ll terminate the algorithm at some point. Otherwise, we could keep going solving sub-problems indefinitely.
So when do we stop solving sub-problems? We can stop as soon as we get to a case which is trivial to solve: a base case. In our case that is when one or both input strings are empty. If both strings are empty then the edit distance between them is 0, because they are already equal. Otherwise, the edit distance will be the length of the string that is not empty. For example, to transform “aab” into “” we can either remove the 3 characters from the first string or insert them into the second string. In any case, the edit distance is 3.
What we have done so far is defining the solution to our problem in terms of the solution to a smaller sub-problem of the same type and identified the base case when we already know what the result is. This should be a clear hint that a recursive algorithm can be applied.
But first, lets translate the three choices discussed previously describing the relationship between sub-problems into something that will be more helpful when trying to code this. The recurrence relation can be defined as:
The first case of the previous formula is when we replace A[0] by B[0], the second one is when we delete A[0] and the last one is when we insert into A. The base cases are:
Notice that the case where both strings are empty is already covered by the first base case because length(A) == length(“”) == 0.
Translating this definition into a recursive algorithm is relatively straightforward:
public class BruteForceEditDistance implements EditDistance {
public int editDistance(String word1, String word2) {
if (word1.isEmpty()) return word2.length();
if (word2.isEmpty()) return word1.length();
int replace = editDistance(word1.substring(1), word2.substring(1)) + Util.replaceCost(word1, word2, 0, 0);
int delete = editDistance(word1.substring(1), word2) + 1;
int insert = editDistance(word1, word2.substring(1)) + 1;
return Util.min(replace, delete, insert);
}
}The Util class has some useful methods that we’ll use on the different implementations of the algorithm and it looks something like this:
public class Util {
/**
* Prevent instantiation
*/
private Util(){}
public static int replaceCost(String w1, String w2, int w1Index, int w2Index) {
return (w1.charAt(w1Index) == w2.charAt(w2Index)) ? 0 : 1;
}
public static int min(int... numbers) {
int result = Integer.MAX_VALUE;
for (int each : numbers) {
result = Math.min(result, each);
}
return result;
}
}The code looks concise and it gives the expected answer. But as you can probably imagine, given that we are talking about dynamic programming, this brute force approach is far from efficient. As with the fibonacci example that we saw on the last post, this algorithm computes the same answer multiple times causing an exponential explosion of different paths that we need to explore.
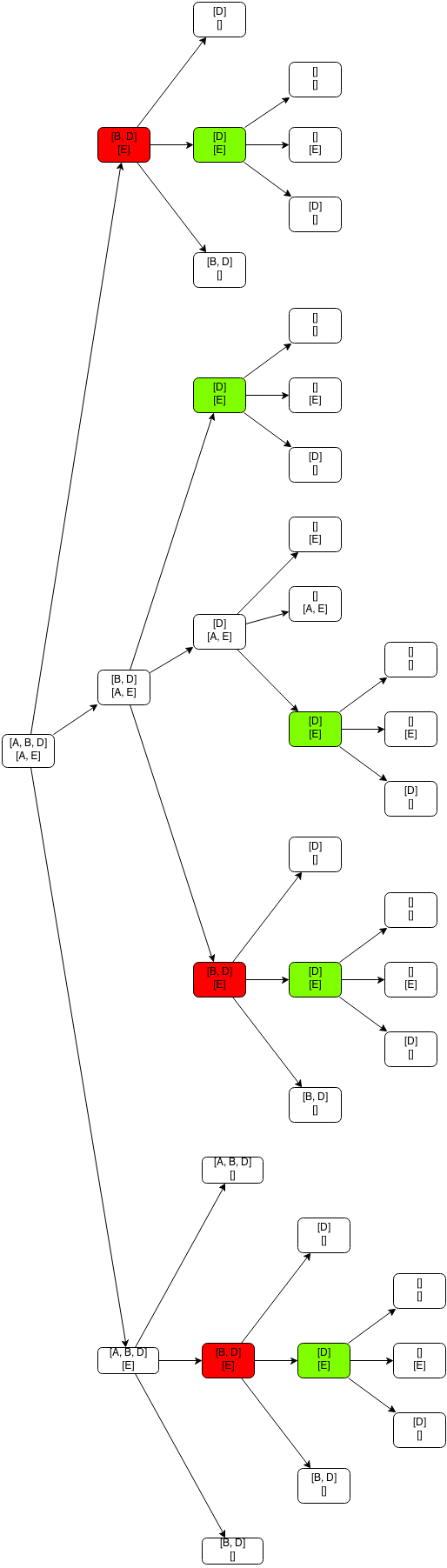
To see this, lets consider the sequence of calls that are made when we invoke this method with word1 = “ABD” and word2 = “AE”:
And that is only for two strings of length 3 and 2. Imagine what that picture looks like when you have proper words or even sentences. In my laptop, for any two strings with 10 or more characters the method never finishes. This approach clearly won’t scale.
So, can we apply dynamic programming to this problem? Remember the two basic properties of a dynamic problem that we discussed in the previous post: overlapping sub-problems and optimal substructure. As we just saw on the example of the previous figure, the edit distance problem clearly has overlapping sub-problems because we are solving smaller sub-problems of the same type to get to the final solution and we need to solve the same sub-problems multiple times.
What about optimal substructure? Can we compute the optimal solution if we have optimal solutions for the sub-problems? Of course! In our case we are trying to minimize the number of transformations, so if we have the optimal solution to the three cases we consider (replace, insert and delete) then we get the minimum from those 3 and that’s our optimal solution.
Remember from the previous post that we could have a top-down dynamic programming approach where we memoize the recursive implementation or a bottom-up approach. The latter tends to be more efficient because you avoid the recursive calls. More importantly, the choice between these two can be the difference between a working and a non-working algorithm if the number of recursive calls you need to make to get to the base case is too large. If this is not a problem, then the choice of which one to use usually depends on personal preference or style. Here’s a possible top-down algorithm first:
public class DPMemoizedEditDistance implements EditDistance {
public int editDistance(String word1, String word2) {
return editDistance(word1, word2, new HashMap<StringTuple, Integer>());
}
private int editDistance(String word1, String word2, Map<StringTuple, Integer> computedSolutions) {
if (word1.isEmpty()) return word2.length();
if (word2.isEmpty()) return word1.length();
StringTuple replaceTuple = new StringTuple(word1.substring(1), word2.substring(1));
StringTuple deleteTuple = new StringTuple(word1.substring(1), word2);
StringTuple insertTuple = new StringTuple(word1, word2.substring(1));
int replace = Util.replaceCost(word1, word2, 0, 0) + transformationCost(replaceTuple, computedSolutions);
int delete = 1 + transformationCost(deleteTuple, computedSolutions);
int insert = 1 + transformationCost(insertTuple, computedSolutions);
int minEditDistance = Util.min(replace, delete, insert);
computedSolutions.put(new StringTuple(word1, word2), minEditDistance);
return minEditDistance;
}
private int transformationCost(StringTuple tuple, Map<StringTuple, Integer> solutions) {
if (solutions.containsKey(tuple)) return solutions.get(tuple);
int result = editDistance(tuple.s1, tuple.s2, solutions);
solutions.put(tuple, result);
return result;
}
/**
* Helper class to save previous solutions
*
*/
private class StringTuple {
private final String s1;
private final String s2;
public StringTuple(String s1, String s2) {
this.s1 = s1;
this.s2 = s2;
}
@Override
public int hashCode() {
return HashCodeBuilder.reflectionHashCode(this);
}
@Override
public boolean equals(Object obj) {
return EqualsBuilder.reflectionEquals(this,obj);
}
}
}Lets see what is going on here. First of all, we are using a Map to store the computed solutions. Since the input to our method are two Strings, we created an auxiliary class with the two Strings that is going to serve as the key to the Map. Our public method has the same interface as before, receiving the 2 inputs and returning the distance. In this memoized version we create the Map here and delegate the calculation to the private method that will make the necessary recursive calls. This private method will use the computedSolutions Map to avoid doing duplicated work. The rest of the algorithm works exactly as the brute force approach we saw before. On each step, we compute (or get the result if it was already computed) the edit distance for the three different possibilities: replace, delete and insert. Now after computing these distances, we save them, take the minimum of them, save the result for the original input and return that.
This algorithm is a huge improvement over the naive recursive one we saw before. Just to give an example, the same invocation that never ended before now takes 0.075 seconds to complete. The good thing about this approach is that we are able to reuse the recursive method that we already had before with some minor modifications. The bad part is that we are doing a lot of comparisons and manipulations of Strings and this tends to be slow.
Since the two strings that we receive as input might be large, lets try to use a bottom-up approach:
public class DPBottomUpEditDistance implements EditDistance {
public int editDistance(String word1, String word2) {
if (word1.isEmpty()) return word2.length();
if (word2.isEmpty()) return word1.length();
int word1Length = word1.length();
int word2Length = word2.length();
//minCosts[i][j] represents the edit distance of the substrings
//word1.substring(i) and word2.substring(j)
int[][] minCosts = new int[word1Length][word2Length];
//This is the edit distance of the last char of word1 and the last char of word2
//It can be 0 or 1 depending on whether the two are different or equal
minCosts[word1Length - 1][word2Length - 1] = Util.replaceCost(word1, word2, word1Length - 1, word2Length - 1);
for (int j = word2Length - 2; j >= 0; j--) {
minCosts[word1Length - 1][j] = 1 + minCosts[word1Length - 1][j + 1];
}
for (int i = word1Length - 2; i >= 0; i--) {
minCosts[i][word2Length - 1] = 1 + minCosts[i + 1][word2Length - 1];
}
for (int i = word1Length - 2; i >= 0; i--) {
for (int j = word2Length - 2; j >= 0; j--) {
int replace = Util.replaceCost(word1, word2, i, j) + minCosts[i + 1][j + 1];
int delete = 1 + minCosts[i + 1][j];
int insert = 1 + minCosts[i][j + 1];
minCosts[i][j] = Util.min(replace, delete, insert);
}
}
return minCosts[0][0];
}
}Here we create a matrix to hold the values of the edit distances of the different substrings. Instead of keeping references to all the different substrings, like we did on the memoized version, we just keep 2 indices. So minCosts[i][j] is the value for the edit distance between word1[i..n] and word2[j..m]. Given this structure, what is the smallest problem for which the solution is trivial? The one that considers the two last characters of each String: if both characters are equal then their edit distance is 0, otherwise is 1.
Lets follow the algorithm through the original example of “cat” and “cars” to better understand how it works. Suppose word1= and word2 =. Then, our matrix will have a size of 3×4 with all places initially set to 0:
Next we compare the two last characters of both Strings, so “t” and “s”. Since they are different we update minCosts[2][3] with 1:
Once we have that value, we can calculate all the other values for the last row and last column. For instance, what does minCosts[2][2] mean? According to our definition is the edit distance between word1[2..2] and word2[2..3], which in our case means the edit distance between “t” and “rs”. But since we already know that the edit distance between “t” and “s” is 1 (because we can look for that value on the matrix) any extra letter we add to the second string while leaving the first one fixed can only increase the distance by 1. So minCosts[2][2] is equal to minCosts[2][3] + 1, minCosts[2][1] is equal to minCosts[2][2] + 1 and minCosts[2][0] is equal to minCosts[2][1] + 1.
The same reasoning applies if we leave the column fixed and move up through the rows. After this two initial loops our matrix looks like this:
Now we can easily fill in our matrix by following the recurrence formula we defined in the beginning. For each cell we will need the value of the cell to its right, the cell directly below and the cell on its right diagonal. So we can traverse the matrix from bottom to top and from right to left. Applying the recurrence formula to minCosts[1][2] for example, we get that its value is 2. With this value we can calculate minCosts[1][1], minCosts[1][0] and the values for the first row. Our final matrix is:
So now that we have all our matrix filled up, what is the answer to our original problem? Remember once again that minCosts[i][j] is the value for the edit distance between word1.substring(i) and word2.substring(j). Therefore, since word1.substring(0) == word1, our final answer is the value sitting at minCosts[0][0].
What are the advantages of this bottom-up approach against the memoized version? First, we don’t need the recursive calls. Our implementation is a completely iterative method that just traverses a matrix. Second, we don’t need to keep track of all the possible substrings and operate on them. We simply use the indices of the matrix to represent the substrings which is considerably faster.
To conclude this post, lets recap what we did in order to solve this problem:
- We identified that we could solve the original problem by splitting it into smaller sub-problems of the same type
- We assumed that we somehow knew what the answers to the sub-problems were and thought about how we would use those answers to get to the answer for the original problem
- From the previous step we defined a general recurrence formula that represented the relationships between the different sub-problems. This recurrence formulation is usually the most important part of solving a dynamic programming formula. Once we have it, translating that into the algorithm is usually straightforward
- We implemented a naive recursive solution and we identified that we were solving the same sub-problems over and over again
- We modified the previous solution to save and reuse the results by using a memoized recursive method
- We identified that the recursive calls could be an issue for long strings and so we developed a bottom-up approach. In this version we defined a matrix to hold the results and we figured in which way we needed to fill it by using the exact same recurrence formula defined before
You can find all the implementations we saw here, together with automated tests for each one showing the differences in execution time on https://github.com/jlordiales/edit-distance
In the next posts we’ll see that this same steps can be applied with minor modifications to a huge amount of different problems. Once you get familiar with the basic tips and tricks of dynamic programming most problems are quite similar.
Cheers!!!

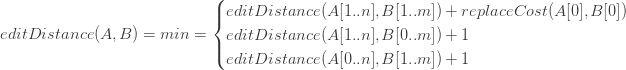
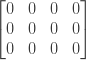
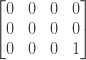
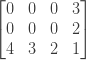
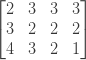




thanks very much for this!
are you planning on doing more examples on dynamic programming?
The algorithm for the Bottom Up scenario is incorrect. Consider the strings word1 = “a” and word2 = “ab”. The minimum edit distance is obviously 1 (just remove ‘b’ at the end of word2), but the above algorithm will give a distance of 2! Let’s follow the algorithm: 1) We build a (very small 1×2) Minimum Cost matrix minCost 2) minCost[0][1] = 1, because the last characters of the strings are not equal (‘a’ is different from ‘b’) 3) minCost[0][0] = minCost[0][1] + 1 = 2, because “any extra letter we add to the second string while leaving the first… Read more »