Graph Processing: Betweeness Centrality – neo4j’s cypher vs graphstream
Last week I wrote about the betweenness centrality algorithm and my attempts to understand it using graphstream and while reading the source I realised that I might be able to put something together using neo4j’s all shortest paths algorithm.
To recap, the betweenness centrality algorithm is used to determine the load and importance of a node in a graph.
While talking about this with Jen she pointed out that calculating the betweenness centrality of nodes across the whole graph often doesn’t make sense. However, it can be useful to know which node is the most important in a smaller sub graph that you’re interested in.
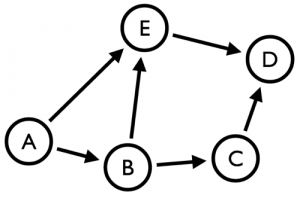
In this case I’m interested in working out the betweenness centrality of nodes in a very small directed graph:
Let’s briefly recap the algorithm:
[Betweenness centrality] is equal to the number of shortest paths from all vertices to all others that pass through that node.
This means that we exclude any paths which go directly between two nodes without passing through any others, something which I didn’t initially grasp.
If we work out the applicable paths by hand we end up with the following:
A -> B: Direct Path Exists A -> C: B A -> D: E A -> E: Direct Path Exists B -> A: No Path Exists B -> C: Direct Path Exists B -> D: E or C B -> E: Direct Path Exists C -> A: No Path Exists C -> B: No Path Exists C -> D: Direct Path Exists C -> E: No Path Exists D -> A: No Path Exists D -> B: No Path Exists D -> C: No Path Exists D -> E: No Path Exists E -> A: No Path Exists E -> B: No Path Exists E -> C: No Path Exists E -> D: Direct Path Exists
Which gives the following betweenness centrality values:
A: 0 B: 1 C: 0.5 D: 0 E: 1.5
We can write a test against the latest version of graphstream (which takes direction into account) to confirm our manual algorithm:
@Test
public void calculateBetweennessCentralityOfMySimpleGraph() {
Graph graph = new SingleGraph("Tutorial 1");
Node A = graph.addNode("A");
Node B = graph.addNode("B");
Node E = graph.addNode("E");
Node C = graph.addNode("C");
Node D = graph.addNode("D");
graph.addEdge("AB", A, B, true);
graph.addEdge("BE", B, E, true);
graph.addEdge("BC", B, C, true);
graph.addEdge("ED", E, D, true);
graph.addEdge("CD", C, D, true);
graph.addEdge("AE", A, E, true);
BetweennessCentrality bcb = new BetweennessCentrality();
bcb.computeEdgeCentrality(false);
bcb.betweennessCentrality(graph);
System.out.println("A="+ A.getAttribute("Cb"));
System.out.println("B="+ B.getAttribute("Cb"));
System.out.println("C="+ C.getAttribute("Cb"));
System.out.println("D="+ D.getAttribute("Cb"));
System.out.println("E="+ E.getAttribute("Cb"));
}The output is as expected:
A=0.0 B=1.0 C=0.5 D=0.0 E=1.5
I wanted to see if I could do the same thing using neo4j so I created the graph in a blank database using the following cypher statements:
CREATE (A {name: "A"})
CREATE (B {name: "B"})
CREATE (C {name: "C"})
CREATE (D {name: "D"})
CREATE (E {name: "E"})
CREATE A-[:TO]->E
CREATE A-[:TO]->B
CREATE B-[:TO]->C
CREATE B-[:TO]->E
CREATE C-[:TO]->D
CREATE E-[:TO]->DI then wrote a query which found the shortest path between all sets of nodes in the graph:
MATCH p = allShortestPaths(source-[r:TO*]->destination) WHERE source <> destination RETURN NODES(p)
If we run that it returns the following:
==> +---------------------------------------------------------+
==> | NODES(p) |
==> +---------------------------------------------------------+
==> | [Node[1]{name:"A"},Node[2]{name:"B"}] |
==> | [Node[1]{name:"A"},Node[2]{name:"B"},Node[3]{name:"C"}] |
==> | [Node[1]{name:"A"},Node[5]{name:"E"},Node[4]{name:"D"}] |
==> | [Node[1]{name:"A"},Node[5]{name:"E"}] |
==> | [Node[2]{name:"B"},Node[3]{name:"C"}] |
==> | [Node[2]{name:"B"},Node[3]{name:"C"},Node[4]{name:"D"}] |
==> | [Node[2]{name:"B"},Node[5]{name:"E"},Node[4]{name:"D"}] |
==> | [Node[2]{name:"B"},Node[5]{name:"E"}] |
==> | [Node[3]{name:"C"},Node[4]{name:"D"}] |
==> | [Node[5]{name:"E"},Node[4]{name:"D"}] |
==> +---------------------------------------------------------+
==> 10 rowsWe’re still returning the direct links between nodes but that’s reasonably easy to correct by filtering the results based on the number of nodes in the path:
MATCH p = allShortestPaths(source-[r:TO*]->destination) WHERE source <> destination AND LENGTH(NODES(p)) > 2 RETURN EXTRACT(n IN NODES(p): n.name)
==> +--------------------------------+ ==> | EXTRACT(n IN NODES(p): n.name) | ==> +--------------------------------+ ==> | ["A","B","C"] | ==> | ["A","E","D"] | ==> | ["B","C","D"] | ==> | ["B","E","D"] | ==> +--------------------------------+ ==> 4 rows
If we tweak the cypher query a bit we can get a collection of the shortest paths for each source/destination:
MATCH p = allShortestPaths(source-[r:TO*]->destination)
WHERE source <> destination AND LENGTH(NODES(p)) > 2
WITH EXTRACT(n IN NODES(p): n.name) AS nodes
RETURN HEAD(nodes) AS source,
HEAD(TAIL(TAIL(nodes))) AS destination,
COLLECT(nodes) AS paths==> +------------------------------------------------------+ ==> | source | destination | paths | ==> +------------------------------------------------------+ ==> | "A" | "D" | [["A","E","D"]] | ==> | "A" | "C" | [["A","B","C"]] | ==> | "B" | "D" | [["B","C","D"],["B","E","D"]] | ==> +------------------------------------------------------+ ==> 3 rows
When we have a way to slice collections using cypher it wouldn’t be too difficult to get from here to a betweenness centrality score for the nodes but for now it’s much easier to use a general programming language.
In this case I used Ruby and came up with the following code:
require 'neography'
neo = Neography::Rest.new
query = " MATCH p = allShortestPaths(source-[r:TO*]->destination)"
query << " WHERE source <> destination AND LENGTH(NODES(p)) > 2"
query << " WITH EXTRACT(n IN NODES(p): n.name) AS nodes"
query << " RETURN HEAD(nodes) AS source, HEAD(TAIL(TAIL(nodes))) AS destination, COLLECT(nodes) AS paths"
betweenness_centrality = { "A" => 0, "B" => 0, "C" => 0, "D" => 0, "E" => 0 }
neo.execute_query(query)["data"].map { |row| row[2].map { |path| path[1..-2] } }.each do |potential_central_nodes|
number_of_central_nodes = potential_central_nodes.size
potential_central_nodes.each do |nodes|
nodes.each { |node| betweenness_centrality[node] += (1.0 / number_of_central_nodes) }
end
end
p betweenness_centralitywhich outputs the following:
$ bundle exec ruby centrality.rb
{"A"=>0, "B"=>1.0, "C"=>0.5, "D"=>0, "E"=>1.5}It seems to do the job but I’m sure there are some corner cases it doesn’t handle which a mature library would take care of. As an experiment to see what’s possible I think it’s not too bad though!
The graph is on the neo4j console in case anyone is interested in playing around with it.






please provide tutorial of neo4js
Hi Mark,
That was a nice article, with clear nice-to-read examples.
Dru